How to Graph Something When You Know the Minimum and Maximum Points

Evidence Mobile Notice Show All NotesHibernate All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.east. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is all-time views in landscape manner. If your device is not in landscape style many of the equations will run off the side of your device (should be able to scroll to encounter them) and some of the menu items volition be cut off due to the narrow screen width.

Section 3-3 : Relative Minimums and Maximums

In this section we are going to extend one of the more important ideas from Calculus I into functions of two variables. We are going to start looking at trying to observe minimums and maximums of functions. This in fact will be the topic of the post-obit two sections likewise.

In this department we are going to be looking at identifying relative minimums and relative maximums. Recollect equally well that we will often use the word extrema to refer to both minimums and maximums.

The definition of relative extrema for functions of ii variables is identical to that for functions of ane variable we but need to remember now that we are working with functions of two variables. So, for the sake of abyss here is the definition of relative minimums and relative maximums for functions of two variables.

Definition

1. A function \(f\left( {x,y} \right)\) has a relative minimum at the point \(\left( {a,b} \correct)\) if \(f\left( {x,y} \right) \ge f\left( {a,b} \right)\) for all points\(\left( {x,y} \right)\) in some region around \(\left( {a,b} \right)\).
2. A function \(f\left( {x,y} \right)\) has a relative maximum at the point \(\left( {a,b} \right)\) if \(f\left( {10,y} \right) \le f\left( {a,b} \right)\) for all points\(\left( {x,y} \right)\) in some region around \(\left( {a,b} \right)\).

Note that this definition does not say that a relative minimum is the smallest value that the function will ever take. Information technology merely says that in some region around the point \(\left( {a,b} \right)\) the function will always be larger than \(f\left( {a,b} \correct)\). Exterior of that region it is completely possible for the role to be smaller. Too, a relative maximum only says that effectually \(\left( {a,b} \right)\) the function will always be smaller than \(f\left( {a,b} \correct)\). Again, outside of the region it is completely possible that the function will be larger.

Next, we need to extend the idea of critical points upward to functions of ii variables. Recall that a critical point of the part \(f\left( x \right)\) was a number \(x = c\) so that either \(f'\left( c \right) = 0\) or \(f'\left( c \right)\) doesn't exist. We have a like definition for disquisitional points of functions of two variables.

Definition

The bespeak \(\left( {a,b} \right)\) is a critical point (or a stationary betoken) of \(f\left( {10,y} \right)\) provided one of the following is true,

1. \(\nabla f\left( {a,b} \right) = \vec 0\) (this is equivalent to proverb that \({f_x}\left( {a,b} \right) = 0\) and \({f_y}\left( {a,b} \right) = 0\)),
2. \({f_x}\left( {a,b} \right)\) and/or \({f_y}\left( {a,b} \right)\) doesn't exist.

To see the equivalence in the offset function let's start off with \(\nabla f = \vec 0\) and put in the definition of each part.

\[\brainstorm{marshal*}\nabla f\left( {a,b} \right) & = \vec 0\\ \left\langle {{f_x}\left( {a,b} \correct),{f_y}\left( {a,b} \correct)} \right\rangle & = \left\langle {0,0} \right\rangle \stop{align*}\]

The only way that these two vectors can exist equal is to accept \({f_x}\left( {a,b} \right) = 0\) and \({f_y}\left( {a,b} \correct) = 0\). In fact, we will use this definition of the critical signal more than the gradient definition since it will be easier to detect the critical points if we start with the fractional derivative definition.

Note equally well that BOTH of the first order partial derivatives must exist zero at \(\left( {a,b} \right)\). If only one of the kickoff order partial derivatives are zero at the point and then the point volition NOT be a critical point.

We now have the post-obit fact that, at least partially, relates critical points to relative extrema.

Fact

If the point \(\left( {a,b} \correct)\) is a relative extrema of the function \(f\left( {x,y} \correct)\) and the offset gild derivatives of \(f\left( {ten,y} \right)\) exist at \(\left( {a,b} \right)\) so \(\left( {a,b} \correct)\) is too a disquisitional point of \(f\left( {ten,y} \correct)\) and in fact nosotros'll have \(\nabla f\left( {a,b} \right) = \vec 0\).

Proof

This is a really simple proof that relies on the unmarried variable version that we saw in Calculus I version, ofttimes called Fermat's Theorem.

Allow's start off by defining \(chiliad\left( ten \right) = f\left( {x,b} \right)\) and suppose that \(f\left( {x,y} \right)\) has a relative extrema at \(\left( {a,b} \right)\). Even so, this also means that \(g\left( x \right)\) too has a relative extrema (of the same kind equally \(f\left( {x,y} \correct)\)) at \(x = a\). By Fermat'south Theorem we then know that \(1000'\left( a \right) = 0\). But we likewise know that \(yard'\left( a \right) = {f_x}\left( {a,b} \right)\) and then we have that \({f_x}\left( {a,b} \right) = 0\).

If we now define \(h\left( y \right) = f\left( {a,y} \right)\) and going through exactly the same process equally above nosotros will see that \({f_y}\left( {a,b} \right) = 0\).

So, putting all this together means that \(\nabla f\left( {a,b} \correct) = \vec 0\) and then \(f\left( {x,y} \right)\) has a disquisitional indicate at \(\left( {a,b} \right)\).

Note that this does Not say that all disquisitional points are relative extrema. It only says that relative extrema volition be critical points of the role. To see this let'southward consider the function

\[f\left( {x,y} \right) = xy\]

The two offset gild partial derivatives are,

\[{f_x}\left( {10,y} \correct) = y\hspace{0.75in}{f_y}\left( {x,y} \right) = x\]

The merely bespeak that will make both of these derivatives zero at the same fourth dimension is \(\left( {0,0} \correct)\) and so \(\left( {0,0} \correct)\) is a critical point for the function. Here is a graph of the role.

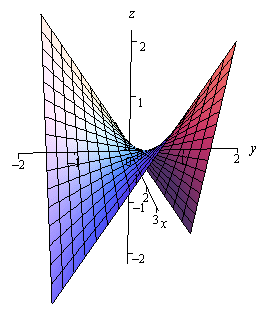
Note that the axes are not in the standard orientation hither so that nosotros can see more conspicuously what is happening at the origin, i.eastward. at \(\left( {0,0} \right)\). If we start at the origin and move into either of the quadrants where both \(ten\) and \(y\) are the aforementioned sign the function increases. Nevertheless, if we start at the origin and motility into either of the quadrants where \(x\) and \(y\) take the opposite sign then the part decreases. In other words, no matter what region you lot take about the origin at that place will be points larger than \(f\left( {0,0} \right) = 0\) and points smaller than \(f\left( {0,0} \right) = 0\). Therefore, there is no way that \(\left( {0,0} \right)\) can be a relative extrema.

Critical points that exhibit this kind of behavior are called saddle points.

While we take to be conscientious to not misinterpret the results of this fact information technology is very useful in helping us to identify relative extrema. Because of this fact we know that if we accept all the critical points of a function so we too have every possible relative extrema for the role. The fact tells us that all relative extrema must be disquisitional points so nosotros know that if the function does have relative extrema and then they must be in the collection of all the critical points. Remember however, that it will be completely possible that at least one of the critical points won't be a relative extrema.

So, once we have all the critical points in hand all we will demand to do is test these points to see if they are relative extrema or not. To determine if a critical point is a relative extrema (and in fact to determine if it is a minimum or a maximum) we can utilize the following fact.

Fact

Suppose that \(\left( {a,b} \right)\) is a critical point of \(f\left( {ten,y} \correct)\) and that the second order partial derivatives are continuous in some region that contains \(\left( {a,b} \correct)\). Next define,

\[D = D\left( {a,b} \right) = {f_{x\,x}}\left( {a,b} \right){f_{y\,y}}\left( {a,b} \right) - {\left[ {{f_{10\,y}}\left( {a,b} \right)} \right]^2}\]

Nosotros then have the following classifications of the critical point.

1. If \(D > 0\) and \({f_{x\,x}}\left( {a,b} \right) > 0\) then at that place is a relative minimum at \(\left( {a,b} \right)\).
2. If \(D > 0\) and \({f_{10\,x}}\left( {a,b} \correct) < 0\) then there is a relative maximum at \(\left( {a,b} \right)\).
3. If \(D < 0\) and then the betoken \(\left( {a,b} \right)\) is a saddle point.
4. If \(D = 0\) then the point \(\left( {a,b} \right)\) may be a relative minimum, relative maximum or a saddle point. Other techniques would need to be used to classify the disquisitional point.

Annotation that if \(D > 0\) so both \({f_{\,x\,x}}\left( {a,b} \right)\) and \({f_{\,y\,y}}\left( {a,b} \right)\) will have the aforementioned sign and so in the beginning two cases above we could just equally easily replace \({f_{\,ten\,x}}\left( {a,b} \right)\) with \({f_{\,y\,y}}\left( {a,b} \right)\). Also annotation that we aren't going to be seeing whatsoever cases in this form where \(D = 0\) as these can oftentimes exist quite difficult to classify. We will be able to classify all the critical points that we find.

Let's meet a couple of examples.

Example i Find and classify all the critical points of \(f\left( {x,y} \correct) = 4 + {ten^3} + {y^3} - 3xy\).

Testify Solution

We offset demand all the starting time order (to find the critical points) and 2d order (to allocate the critical points) partial derivatives so let's become those.

\[\begin{array}{c}{f_x} = 3{ten^two} - 3y\hspace{0.5in}{f_y} = 3{y^two} - 3x\\ {f_{x\,x}} = 6x\hspace{0.5in}{f_{y\,y}} = 6y\hspace{0.5in}{f_{x\,y}} = - 3\end{assortment}\]

Let'southward beginning find the critical points. Disquisitional points volition be solutions to the system of equations,

\[\begin{align*}{f_x} & = iii{ten^2} - 3y = 0\\ {f_y} & = 3{y^ii} - 3x = 0\end{align*}\]

This is a not-linear system of equations and these tin can, on occasion, be difficult to solve. However, in this case it's not too bad. We tin can solve the first equation for \(y\) equally follows,

\[three{10^ii} - 3y = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}y = {ten^2}\]

Plugging this into the second equation gives,

\[3{\left( {{x^ii}} \right)^2} - 3x = 3x\left( {{ten^3} - 1} \right) = 0\]

From this we can meet that nosotros must have \(x = 0\) or \(x = 1\). Now utilize the fact that \(y = {x^ii}\) to get the disquisitional points.

\[\begin{align*}x = 0: & \hspace{0.25in}y = {0^2} = 0\hspace{0.1in} & \Rightarrow & \hspace{0.5in}\left( {0,0} \right)\\ ten = 1: & \hspace{0.25in}y = {i^ii} = 1\hspace{0.1in} & \Rightarrow & \hspace{0.5in}\left( {1,1} \correct)\stop{align*}\]

So, nosotros get two disquisitional points. All we need to do now is classify them. To exercise this we will need \(D\). Here is the general formula for \(D\).

\[\begin{align*}D\left( {ten,y} \correct) & = {f_{x\,x}}\left( {x,y} \right){f_{y\,y}}\left( {x,y} \correct) - {\left[ {{f_{ten\,y}}\left( {x,y} \right)} \right]^two}\\ & = \left( {6x} \right)\left( {6y} \right) - {\left( { - 3} \right)^two}\\ & = 36xy - 9\finish{marshal*}\]

To classify the critical points all that nosotros need to do is plug in the critical points and use the fact in a higher place to classify them.

\(\left( {0,0} \right)\) : \[D = D\left( {0,0} \correct) = - 9 < 0\]

And so, for \(\left( {0,0} \right)\) \(D\) is negative and so this must be a saddle signal.

\(\left( {1,ane} \correct)\) : \[D = D\left( {1,i} \correct) = 36 - 9 = 27 > 0\hspace{0.5in}{f_{x\,x}}\left( {one,ane} \right) = six > 0\]

For \(\left( {1,one} \right)\) \(D\) is positive and \({f_{x\,ten}}\) is positive and so we must accept a relative minimum.

For the sake of completeness here is a graph of this function.

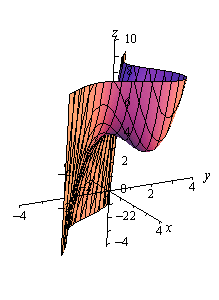
Notice that in society to get a better visual we used a somewhat nonstandard orientation. We can see that in that location is a relative minimum at \(\left( {1,1} \right)\) and (hopefully) it'south clear that at \(\left( {0,0} \right)\) we do get a saddle point.

Example 2 Discover and classify all the disquisitional points for \(f\left( {10,y} \correct) = 3{10^ii}y + {y^3} - 3{ten^2} - 3{y^two} + ii\)

Bear witness Solution

Every bit with the first example we will first need to get all the offset and second order derivatives.

\[\brainstorm{assortment}{c}{f_x} = 6xy - 6x\hspace{0.5in}{f_y} = 3{x^2} + three{y^2} - 6y\\ {f_{x\,x}} = 6y - half dozen\hspace{0.5in}{f_{y\,y}} = 6y - 6\hspace{0.75in}{f_{10\,y}} = 6x\end{array}\]

We'll first need the critical points. The equations that we'll need to solve this fourth dimension are,

\[\begin{marshal*}6xy - 6x & = 0\\ three{10^2} + iii{y^2} - 6y & = 0\end{align*}\]

These equations are a little trickier to solve than the first set, just one time you run into what to do they actually aren't terribly bad.

Starting time, let's notice that nosotros can factor out a 6\(x\) from the first equation to get,

\[6x\left( {y - i} \right) = 0\]

And then, we can meet that the first equation volition be zero if \(x = 0\) or \(y = i\). Be careful to not just cancel the \(10\) from both sides. If we had done that we would accept missed \(ten = 0\).

To discover the critical points we can plug these (individually) into the 2nd equation and solve for the remaining variable.

\(x = 0\) : \[3{y^2} - 6y = 3y\left( {y - 2} \right) = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}y = 0,\,\,y = 2\] \(y = 1\) : \[3{x^2} - 3 = 3\left( {{x^2} - 1} \right) = 0\hspace{0.5in} \Rightarrow \hspace{0.25in}10 = - i,\,\,ten = one\]

So, if \(x = 0\) we have the following critical points,

\[\left( {0,0} \right)\hspace{0.25in}\left( {0,ii} \right)\]

and if \(y = i\) the critical points are,

\[\left( {1,1} \right)\hspace{0.25in}\left( { - 1,ane} \correct)\]

Now all we need to exercise is allocate the critical points. To exercise this nosotros'll need the general formula for \(D\).

\[D\left( {x,y} \right) = \left( {6y - 6} \right)\left( {6y - six} \correct) - {\left( {6x} \right)^2} = {\left( {6y - vi} \right)^2} - 36{ten^2}\] \(\left( {0,0} \right)\) : \[D = D\left( {0,0} \right) = 36 > 0\hspace{0.5in}{f_{x\,ten}}\left( {0,0} \right) = - vi < 0\] \(\left( {0,ii} \right)\) : \[D = D\left( {0,2} \right) = 36 > 0\hspace{0.5in}{f_{x\,x}}\left( {0,ii} \right) = 6 > 0\] \(\left( {ane,i} \right)\) : \[D = D\left( {i,1} \correct) = - 36 < 0\] \(\left( { - ane,1} \right)\) : \[D = D\left( { - 1,1} \right) = - 36 < 0\]

So, it looks similar we have the following nomenclature of each of these critical points.

\[\begin{align*} & \left( {0,0} \right) & & :\hspace{0.5in}{\mbox{Relative Maximum}}\\ & \left( {0,2} \right) & & : \hspace{0.5in} {\mbox{Relative Minimum}}\\ & \left( {ane,ane} \correct) & & :\hspace{0.5in}{\mbox{Saddle Betoken}}\\ & \left( { - one,1} \right) & & :\hspace{0.5in}{\mbox{Saddle Point}}\stop{marshal*}\]

Hither is a graph of the surface for the sake of completeness.

Let's exercise one more than instance that is a piddling different from the start two.

Case 3 Determine the point on the plane \(4x - 2y + z = i\) that is closest to the point \(\left( { - 2, - 1,5} \right)\).

Show Solution

Annotation that nosotros are NOT request for the disquisitional points of the plane. In social club to practise this example nosotros are going to demand to first come with the equation that we are going to have to work with.

First, let's suppose that \(\left( {10,y,z} \right)\) is any point on the plane. The altitude between this betoken and the point in question, \(\left( { - two, - 1,5} \right)\), is given by the formula,

\[d = \sqrt {{{\left( {10 + two} \correct)}^2} + {{\left( {y + 1} \right)}^2} + {{\left( {z - five} \right)}^2}} \]

What nosotros are and then asked to notice is the minimum value of this equation. The bespeak \(\left( {x,y,z} \correct)\) that gives the minimum value of this equation will exist the betoken on the airplane that is closest to \(\left( { - ii, - 1,5} \right)\).

At that place are a couple of problems with this equation. First, it is a role of \(x\), \(y\) and \(z\) and we can simply deal with functions of \(x\) and \(y\) at this point. All the same, this is piece of cake to ready. We can solve the equation of the aeroplane to run across that,

\[z = one - 4x + 2y\]

Plugging this into the distance formula gives,

\[\begin{align*}d & = \sqrt {{{\left( {ten + 2} \correct)}^ii} + {{\left( {y + 1} \right)}^2} + {{\left( {1 - 4x + 2y - 5} \right)}^2}} \\ & = \sqrt {{{\left( {x + 2} \correct)}^2} + {{\left( {y + 1} \right)}^2} + {{\left( { - 4 - 4x + 2y} \right)}^2}} \cease{align*}\]

Now, the next upshot is that at that place is a square root in this formula and we know that we're going to be differentiating this eventually. And then, in order to make our life a fiddling easier allow'south notice that finding the minimum value of \(d\) will exist equivalent to finding the minimum value of \({d^two}\).

So, allow's instead find the minimum value of

\[f\left( {x,y} \correct) = {d^2} = {\left( {x + ii} \correct)^2} + {\left( {y + 1} \right)^2} + {\left( { - iv - 4x + 2y} \right)^2}\]

Now, we need to be a little careful here. We are being asked to detect the closest point on the plane to \(\left( { - 2, - 1,5} \right)\) and that is non actually the same thing as what we've been doing in this department. In this department we've been finding and classifying disquisitional points as relative minimums or maximums and what nosotros are really request is to find the smallest value the function will take, or the absolute minimum. Hopefully, it does brand sense from a concrete standpoint that there will be a closest point on the plane to \(\left( { - 2, - one,5} \correct)\). This indicate should also be a relative minimum in addition to being an accented minimum.

And then, let's become through the process from the showtime and second example and see what we get equally far as relative minimums go. If nosotros only get a single relative minimum and then we will be done since that point volition also need to exist the absolute minimum of the role and hence the indicate on the plane that is closest to \(\left( { - 2, - 1,5} \right)\).

Nosotros'll demand the derivatives starting time.

\[\begin{align*}{f_x} & = 2\left( {x + 2} \right) + two\left( { - 4} \correct)\left( { - 4 - 4x + 2y} \right) = 36 + 34x - 16y\\ {f_y} & = 2\left( {y + one} \right) + 2\left( 2 \right)\left( { - 4 - 4x + 2y} \right) = - fourteen - 16x + 10y\\ {f_{x\,ten}} & = 34\\ {f_{y\,y}} & = 10\\ {f_{ten\,y}} & = - xvi\terminate{marshal*}\]

Now, before we become into finding the critical point allow's compute \(D\) apace.

\[D = 34\left( {10} \correct) - {\left( { - 16} \correct)^two} = 84 > 0\]

So, in this instance \(D\) will always be positive and likewise notice that \({f_{x\,x}} = 34 > 0\) is always positive and so any critical points that we get will be guaranteed to exist relative minimums.

Now let's find the critical indicate(s). This will hateful solving the organization.

\[\begin{align*}36 + 34x - 16y & = 0\\ - 14 - 16x + 10y & = 0\end{marshal*}\]

To do this we can solve the first equation for \(x\).

\[x = \frac{1}{{34}}\left( {16y - 36} \right) = \frac{1}{{17}}\left( {8y - 18} \right)\]

At present, plug this into the second equation and solve for \(y\).

\[ - xiv - \frac{{16}}{{17}}\left( {8y - 18} \correct) + 10y = 0\hspace{0.5in} \Rightarrow \hspace{0.5in}y = - \frac{{25}}{{21}}\]

Back substituting this into the equation for \(x\) gives \(x = - \frac{{34}}{{21}}\).

So, information technology looks like we get a single disquisitional point : \(\left( { - \frac{{34}}{{21}}, - \frac{{25}}{{21}}} \right)\). Also, since we know this will be a relative minimum and it is the just critical point nosotros know that this is likewise the \(x\) and \(y\) coordinates of the point on the plane that nosotros're after. We can find the \(z\) coordinate past plugging into the equation of the plane as follows,

\[z = 1 - 4\left( { - \frac{{34}}{{21}}} \correct) + 2\left( { - \frac{{25}}{{21}}} \correct) = \frac{{107}}{{21}}\]

And so, the betoken on the plane that is closest to \(\left( { - two, - 1,v} \correct)\) is \(\left( { - \frac{{34}}{{21}}, - \frac{{25}}{{21}},\frac{{107}}{{21}}} \right)\).

benbowhourson.blogspot.com

Source: https://tutorial.math.lamar.edu/classes/calciii/relativeextrema.aspx

Share this post